Gazebo/MoveIt のための 3D モデリング（５）滑らかなサーフェス – 知識編

著者:yamamoto.yosuke

CAD, control point, curvature, degree, Gazebo, MoveIt!, Rhinoceros, surface, サーフェス, シミュレーション, ロボット, 制御点, 曲率, 次数

Gazebo/MoveIt のための 3D モデリング（５）滑らかなサーフェス – 知識編

前回 「Gazebo/MoveIt のための 3D モデリング（３）基本形状編 – その２」 では洗濯機の基本的な形状で構成されるサーフェスのモデリングを行いました．

今回は発展的な内容として滑らかなサーフェスのモデリングに向けた予備知識的な内容の説明をします．

ロボットモデルはシミュレータ上で使うために結局メッシュ（ポリゴン）にしてしまうのでシミュレーションなどに利用する 3D モデル作成においては 「滑らかなサーフェス」 である必要性は高くありません．

しかし，モデリング対象の中には滑らかなサーフェスになるように設計されている製品もあります．そのような製品のモデリングの際に対象物の形状が円弧のように見えるけど何か違うので合わなくて悩むようなことがあります．そういったときに円弧などの基本的な形状以外のサーフェスもあることを知っていると，それは厳密には合わないものとして割り切って近似的に円弧などのシンプルな形状としてモデリングするということも適切に判断できると思います．

このようなことから，今回の記事はそういった 「滑らかなサーフェス」 について 「知る」 ことを目的としています．

「滑らか」とは？

「滑らか」 とはは何であるかというと，曲線やサーフェスの位置や接線方向，曲率，曲率の変化率に連続性があるということです．

上の図は 90° の角度をもつ直線間を曲線で接続させたときの連続性の違いによる曲率（黄色カーブ）のグラフ（CurvatureGraph）を表した画像をアニメーション化したものです．
（クリックで拡大）

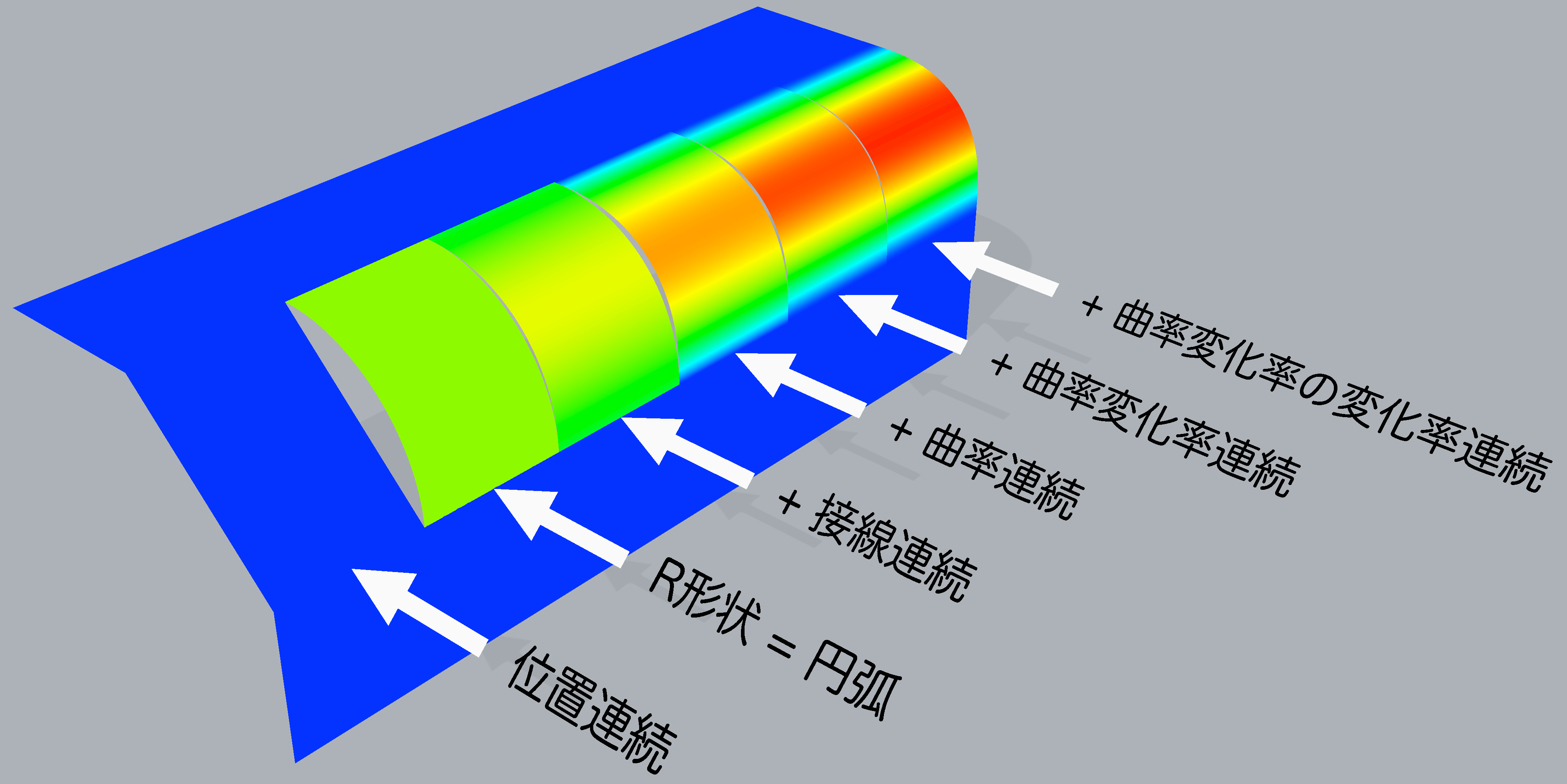
各接続条件は次のリストのように連続性の条件が加わってゆくように考えてください．
「R形状」は「接線連続」のうち円弧で接続できる特殊なケースと捉えることができます．

1. 位置連続
2. 位置連続 + 接線連続
3. 位置連続 + 接線連続 + 曲率連続
4. 位置連続 + 接線連続 + 曲率連続 + 曲率変化率連続
5. 位置連続 + 接線連続 + 曲率連続 + 曲率変化率連続 + 曲率変化率の変化率連続

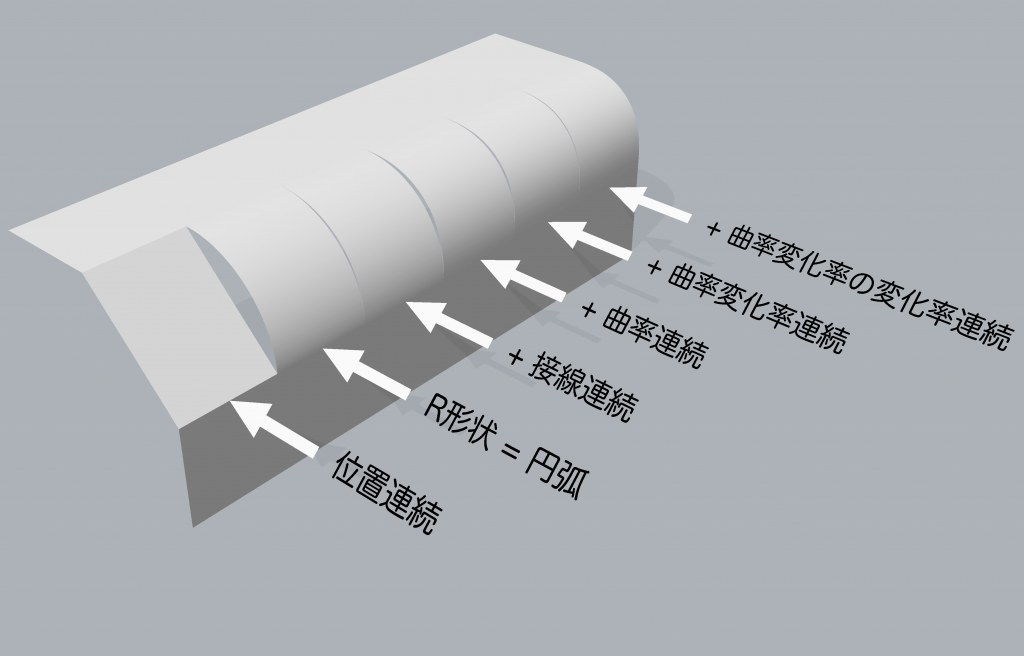
上の図の接続連続性の異なる曲線を 「押し出し」 してサーフェスを作成してレンダリング表示にしたものが次の図です．

影の付き方が曲率や曲率変化率などの連続条件を加えてゆくと段々と滑らかになるのが見て取れるでしょうか？

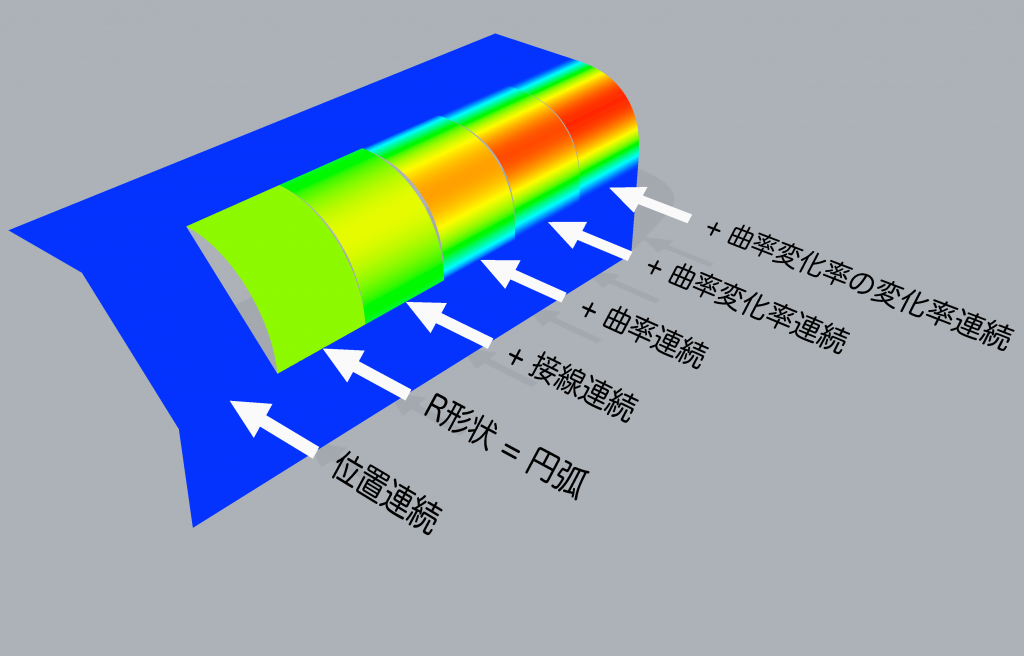
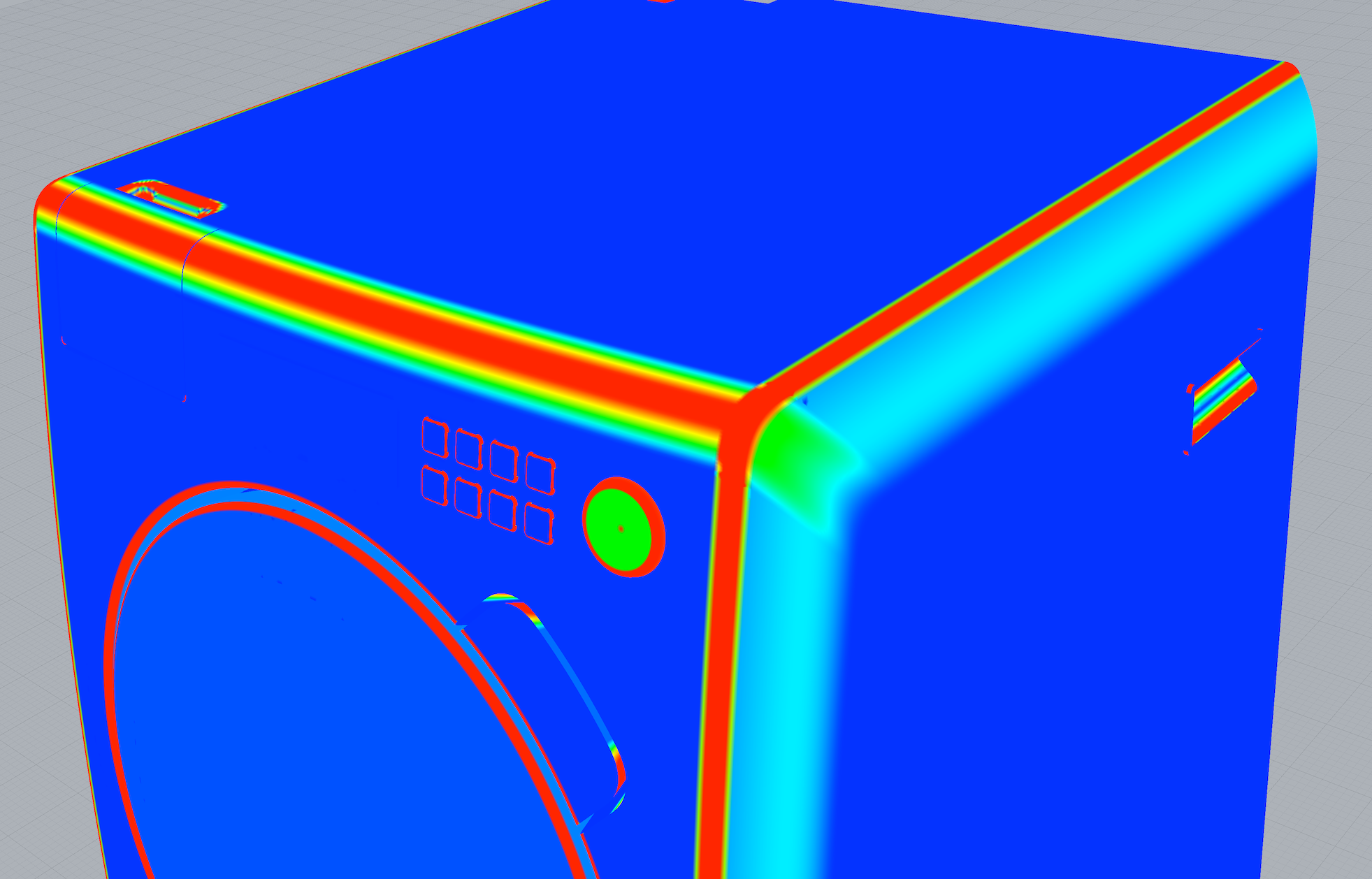
サーフェスの曲率を解析して色で表した（CurvatureAnalysis）ものが次の図で，青が曲率が小さく，赤が曲率が大きいコンタ図になっています．

連続性の条件が加わるにつれて接続部周辺の曲率の変化が緩やかになっています．

また，サーフェスの滑らかさを評価するために 「ゼブラ（縞模様・Zebra）」 解析もわかりやすいのでよく利用します．

• Zebra
• “Zebraコマンドは，縞模様を使用して，サーフェスの滑らかさと連続性を視覚的に評価します．”
• https://docs.mcneel.com/rhino/7/help/ja-jp/commands/zebra.htm

ゼブラ表示によりサーフェスの連続性がより強調されます．縞模様の通り方の滑らかさがサーフェスの接続性の滑らかさを表しています．サーフェスが滑らかに接続しているかどうかを評価したり，接続を滑らかに修正する際に役立ちます．

本シリーズの記事のモデリング対象として作成した洗濯機モデルの曲率とゼブラを表示したものが次の２つの図です．モデル全体で解析すると解析用のメッシュを細かく出来なくなるので，実際には接続性を評価する面に限って解析用メッシュをなるべく細かくして解析をするようにしています．

「制御点」と「次数」

実際に滑らかなサーフェスをモデリングする場合は，サーフェスが CAD やサーフェスモデラ内部でどのように表現されているかを理解しているとより意図したものに近いサーフェスを作成できるように思います．

Rhinoceros や一般的な CAD などでは曲線やサーフェスは NURBS (Non-Uniform Rational B-Spline／非一様有理Bスプライン) という数学的モデルで表現されています．

NURBS 以外にもサーフェスの 3D 表現モデルとして SubD （Subdivision／細分割曲面） もあります． SubD はコンピュータグラフィックス系の 3D モデリングソフトウェアで利用されていますが，機構設計分野ではあまり使われていませんので本シリーズの記事の対象としません．

NURBS で表現される曲線やサーフェスが何で構成されているかは大まかに述べますと 「制御点」 と 「次数」 です．

上の図は前項目で 90° の角度をもつ直線間を連続性の異なる接続をした曲線がそれぞれどのような 「制御点」 と 「次数」 で表現されているかを示した図をアニメーション化したものです．

NURBS カーブにおいてはその接続における連続性は次のリストにある各数の「制御点」により構成されています．

1. 位置連続 → 端点の 1 点
2. 接線連続 → 端点を含めたの 2 点
3. 曲率連続 → 端点を含めたの 3 点
4. 曲率変化率連続 → 端点を含めたの 4 点
5. 曲率変化率の変化率連続 → 端点を含めたの 5 点

「次数（degree）」 は大きな数字になるほど曲線が滑らかになります．

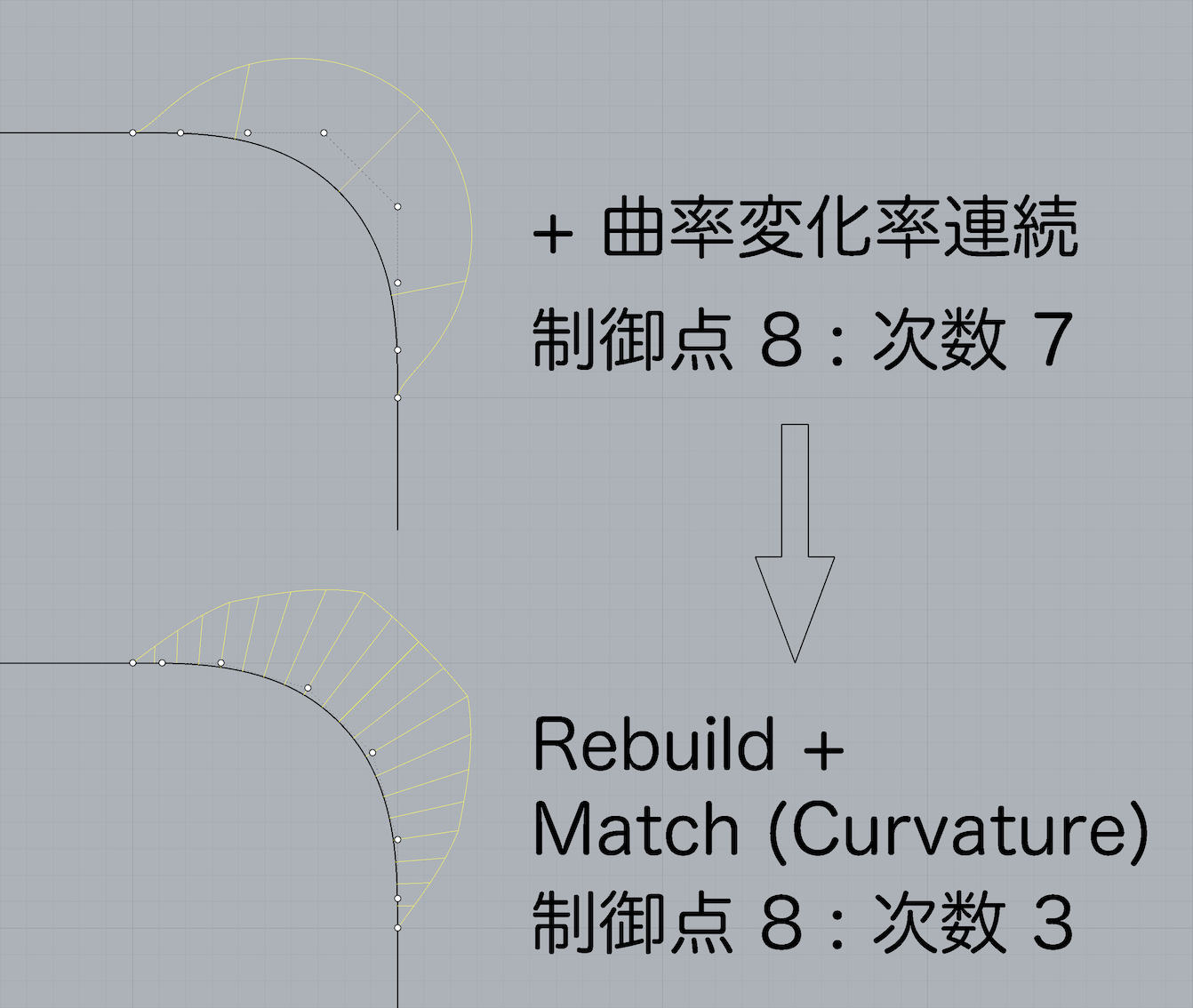
上の図は 90° の角度をもつ直線間を接続した 「制御点:8 次数7 の曲線（曲率変化率連続）」 をあえて 「リビルド（Rebuild）」 して 「制御点:8 次数: 3 の曲線」 にして両端点の曲率を接続先の直線に 「マッチング（Match）」 した曲線の曲率の比較です．同じ制御点数でも次数が低いと曲線内で曲率の変化率の連続性が保てなくなってしまいます．

曲線に設定できる 「次数の最大値」 は 「制御点数 – 1」 です．

両端を曲率連続にするための 「制御点が6個」 の曲線の場合は 「次数の最大値は5次」，両端を曲率変化率連続にするための 「制御点が8個」 の場合は設定できる 「次数の最大値は7次」 になります．

制御点が多いとより細かく曲線やサーフェスの形状の制御が出来ますが，編集が大変だったり，データサイズが大きくなってしまうので，最小の制御点と適切な次数で表現したい形状や滑らかさを規定できるのがベストです．

接続条件は曲線の両端で同じである必要はないので，例えば片方の端は 「位置連続」 にして，もう片方の端は 「曲率変化率連続」 にするということも可能です．この場合の必要最小限の制御点は 「位置連続側: 1点」 と 「曲率変化率連続側: 4点」 と合わせて 「5点」 は必要になります．制御点を 「5点」 とした場合の次数の最大値を採って 「4次」 とするのが良いでしょう．

制御点が少なくて意図する形状が得られないようでしたら適宜制御点を多くして，次数もそれに合わせて大きくすると良いですが，次数の方は最大でも 「７次」 で十分なように筆者は考えています．

サーフェスにおける「制御点」と「次数」

これまで曲線を例に 「制御点」 と 「次数」 について説明してきましたが，サーフェスは曲線の「制御点」と「次数」を2方向に拡張したものです．

サーフェスは 「U方向」 と 「V方向」 の２方向がある 「四角い布」 をベースに，それを伸縮・曲げを行ったり，トリムしてその一部を使ったりするイメージとして捉えることができます．

円錐体のような三角形のサーフェスもありますが 「四角い布」 の特殊例と捉えることができ，同様にUV方向それぞれの要素があります．

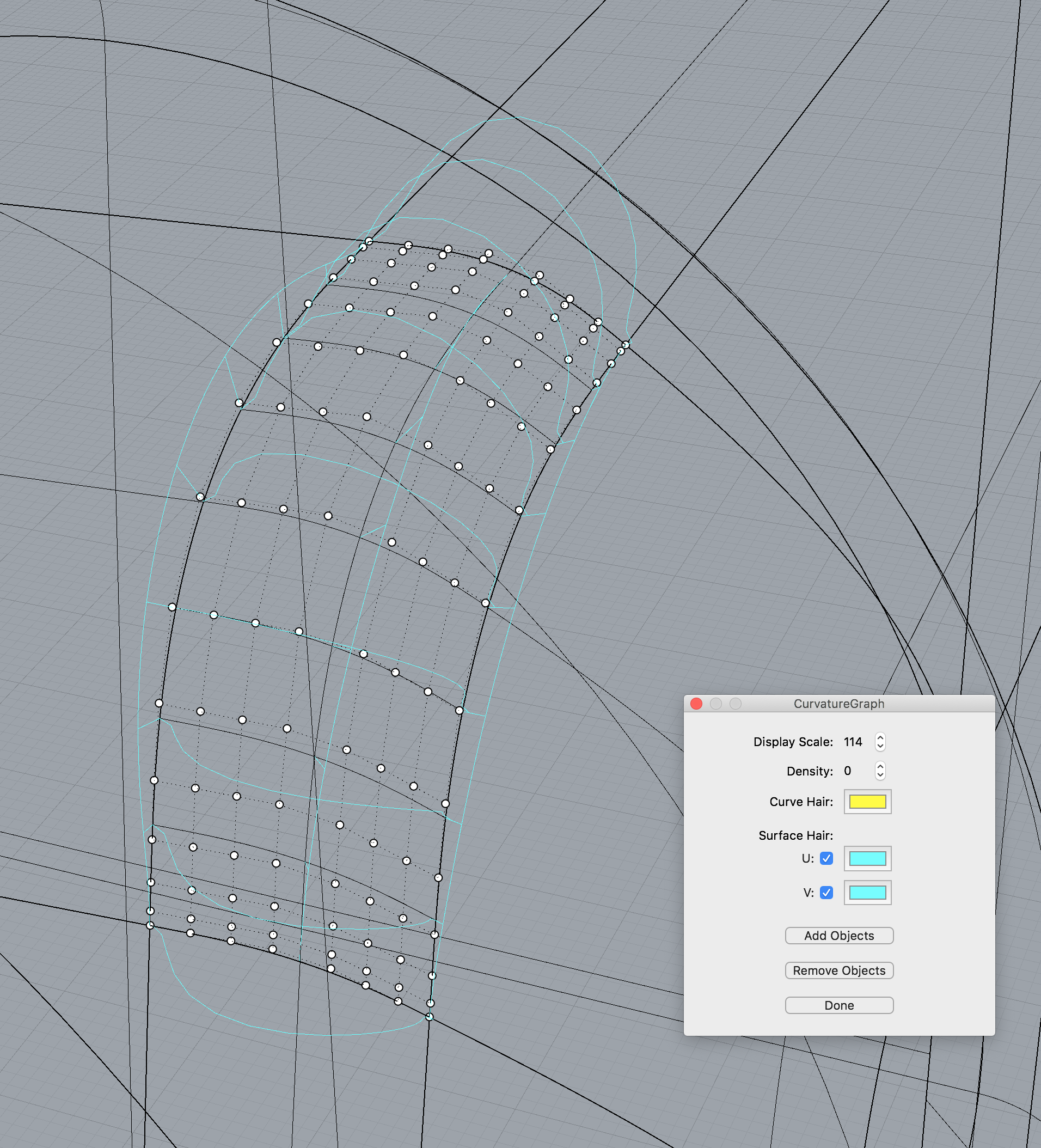
次の図は本シリーズでモデリング対象とするために作成した洗濯機モデルのボディの角部のサーフェスの制御点と曲率のグラフを表示したものです．四方にある接続先のサーフェスとそれぞれ（なるべく）曲率変化率まで連続するように作成しました．そのため次数を 7次 とし，制御点を U方向に 15点，V方向に 8点 を持つサーフェスとしました．

• 図示したサーフェス例の制御点と次数
• U方向: 制御点 15点 / 次数 7
• V方向: 制御点 8点 / 次数 7

曲線の連続性と同じように，サーフェスの連続性も各辺毎に作成時設定できるサーフェスもありますし，マッチングの際に異なる設定で各辺で行えば可能ですが，四辺の接続先と矛盾がないようにしないと隙間のないサーフェスにならない可能性もある点が曲線に比べて難しいところです．

どれほど滑らかにする？

さて，ロボットシミュレータのための 3D モデリングにおいてはどれほど滑らかなサーフェスを作成したら良いのでしょうか？

本記事冒頭で述べたように，ロボットモデルはシミュレータ上で使うために結局メッシュ（ポリゴン）にしてしまうのでシミュレーションなどに利用する 3D モデル作成においては 「滑らかなサーフェス」 である必要性は高くありません．

曲率連続や曲率変化率連続のサーフェスでモデリングしてメッシュ化してもそのような連続性に近い状態を維持しようとするとメッシュが細かくなりデータが重くなります．ただ，そのロボットシミュレーションをデモンストレーションやプレゼンテーションで綺麗に見せたく，少しメッシュデータが重くても良いような場合はなるべく滑らかなサーフェスをモデリングすることもあるように思います．

また，メッシュのデータ量の他にモデル作成の手間も考えておくべきでしょう．

下のリストにサーフェスの連続性の違いをまとめました．技術的なロボットシミュレーションが目的であれば 接線連続 までとしてモデリング時間を省くのも1つの方法です．大きな面はメッシュで形状が潰れてしまわないので 曲率連続 や 曲率変化率連続 まで考慮したモデルとして，小さな面はメッシュ形状に埋もれてしまうので R形状 や 接線連続 としてメリハリをつけるのも良いでしょう．

Rhinoceros では「曲率連続」までは標準の機能として普通に利用できるのでロボットシミュレータのための 3D モデリングでも用いるのはそんなに手間のかかることではないように思います．

1. 位置連続
• 面取り形状など
• 機械設計的
2. R形状
• 隅R・角Rや．前回の記事で作成したフィレットのロフトなどが例
• フライスや旋盤で機械加工された対象物のモデリングには必須
• 機械設計的
3. 接線連続
• ロボット 3D モデリングの自由曲面では多く使う場合が多いか？
4. 曲率連続
• 滑らかに見えるサーフェス
• デザイン的
• 使っている CAD やサーフェイスモデラで機能的に簡単に作成できるようだったら用いてみるのもあり
• Rhinoceros では
• 標準で曲率連続にサーフェフをマッチング修正する機能がある
5. 曲率変化率連続
• より滑らかに見えるサーフェス
• ロボット 3D モデリングでは知識として持っていたら十分
• 使えると造形できるものが増える
• デザイン的
• Rhinoceros では
• 「作成時」に曲率変化率連続性のある曲線・サーフェスを作成する機能はある
• 「修正時」は曲率連続マッチング機能を利用した後に，加えて曲率目視で4番目の制御各点を手動調整する必要があるので手間
• （この曲率変化率連続マッチングを行う Plug-in があれば筆者にも教えて欲しい！）
6. 曲率変化率の変化率連続
• Rhinoceros では
• 「作成時」に曲率変化率の変化率連続性のある曲線・サーフェスを作成する機能はある
• 「修正時」に曲率目視で5番目の制御点まで手動調整するのは難しいか？

今回の記事はここまでです．

大体どのような滑らかさのサーフェスの種類があって，CAD やサーフェスモデラでそれを作成するために必要な条件や作成の手間のイメージが伝わっていると良いのですが．

本シリーズ次回の記事は

「Gazebo/MoveIt のための 3D モデリング（６）滑らかなサーフェス – 作成編」

を予定しています．